Appelons espace étalé au dessus d’un espace topologique tout homéomorphisme local
. Par exemple, si l’on étale une surface de Nutella sur une surface de pain, on obtient un espace étalé au dessus d’un autre (et c’est même un homéomorphisme). L’identité
est toujours un espace étalé (on a étalé une copie de
au dessus de
) :
Il est facile de donner un exemple d’espace étalé qui n’est pas un homéomorphisme : on peut considérer l’injection canonique d’un ouvert :
Et si l’on veut un exemple d’espace étalé surjectif qui n’est pas un homéomorphisme, il suffit de considérer l’application canonique . On a étalé deux copies de
au dessus de
:
Il est un peu moins facile de donner un exemple d’espace étalé connexe qui n’est pas un homéomorphisme. L’exemple classique est l’application définie par
(enroulement de la droite autour du cercle). :
Voici l’exercice : Montrer que tout espace étalé séparé connexe et surjectif au dessus de est injectif.
Remarque 1. Un tel espace étalé est donc un homéomorphisme.
Remarque 2. Si l’on sait des choses sur la simple connexité, par exemple si l’on admet que est simplement connexe, l’exercice est sans doute trivial. mais le but du jeu est de donner une preuve n’utilisant que les résultats basiques de topologie générale sur la connexité et la compacité.
Remarque 3. Voici le code LaTeX qui permet d’obtenir les dessins ci-dessus :
\documentclass{minimal}
\usepackage{amsmath}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}
\fill[black!30] (0,0) ellipse (2 and 0.5);
\path[black,->,>=stealth] (0,3) edge node[auto]{$\mathrm{id}$} (0,0.2) ;
\fill[black!50] (0,3) ellipse (2 and 0.5);
\end{tikzpicture}
\begin{tikzpicture}
\fill[black!30] (0,0) ellipse (2 and 0.5);
\path[black,->,>=stealth] (-0.5,3) edge node[auto]{$i$} (-0.5,0.2) ;
\fill[black!50] (-0.5,3) ellipse (1 and 0.3);
\end{tikzpicture}
\begin{tikzpicture}
\fill[black!30] (0,0) ellipse (2 and 0.5);
\path[black,->,>=stealth] (0,3) edge node[auto]{$\mathrm{id}\sqcup\mathrm{id}$} (0,0.2) ;
\fill[black!50] (0,3) ellipse (2 and 0.5);
\fill[black!60] (0,3.7) ellipse (2 and 0.5);
\end{tikzpicture}
\begin{tikzpicture}
\draw[black,very thick] (0,0) ellipse (2 and 0.5);
\path[black,->,>=stealth] (0,3) edge node[auto]{$f(t)=\exp(it)$} (0,0.2) ;
\draw[very thick,domain=0:720,smooth,variable=\t,samples=150] plot ({2*sin(\t)},3+\t/400,{1*cos(\t)});
\end{tikzpicture}
\end{document}





Ne faut-il pas au moins supposer l’espace étalé séparé?
Sans doute, car je suppose que la séparation n’est pas conservée par homéomorphisme local. Il faut que je relise ma preuve pour voir où elle doit intervenir. Un contre exemple est fourni par la droite avec origine dédoublée (on prend l’union disjointe et on identifie chaque réel du premier
et on identifie chaque réel du premier  avec le réel correspondant dans le second
avec le réel correspondant dans le second  , sauf les origines), c’est bien ça ?
, sauf les origines), c’est bien ça ?
Il me semble.
Voici ce que je propose. Appelons section d’une espace étalé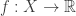 un couple
un couple 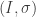 formé d’un intervalle ouvert
formé d’un intervalle ouvert  et d’une application continue
et d’une application continue 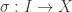 telle que
telle que 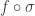 soit l’identité dans l’intervalle.
soit l’identité dans l’intervalle.
a) Deux sections qui sont égales en un
qui sont égales en un 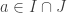 coïncident dans
coïncident dans 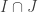 . De fait, l’ensemble non vide (il contient
. De fait, l’ensemble non vide (il contient  )
)  des points en lesquelles elles prennent la même valeur est fermé (car
des points en lesquelles elles prennent la même valeur est fermé (car  est séparé) et ouvert car
est séparé) et ouvert car  est un homéomorphisme local. Pour ce dernier point, notons
est un homéomorphisme local. Pour ce dernier point, notons  un ouvert de
un ouvert de  contenant l’image d’un point de
contenant l’image d’un point de  par les sections et dans lequel
par les sections et dans lequel 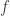 est injectif. Par continuité, il y a un intervalle
est injectif. Par continuité, il y a un intervalle  dont les images par les sections sont incluses à cet ouvert. Comme
dont les images par les sections sont incluses à cet ouvert. Comme  y est injectif,
y est injectif,  . Au total
. Au total 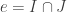 par connexité des intervalles.
par connexité des intervalles.
b) Pour tout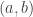 tel que
tel que 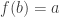 , il y a une section maximale (ie dont le domaine de définition est maximal pour l’inclusion) qui passe par
, il y a une section maximale (ie dont le domaine de définition est maximal pour l’inclusion) qui passe par  en
en  . C’est clair: il y a au moins une section qui passe par
. C’est clair: il y a au moins une section qui passe par  en
en  (car
(car  est un homéomorphisme local surjectif). On prend alors pour domaine de la section cherchée l’union de ceux des sections qui passent par
est un homéomorphisme local surjectif). On prend alors pour domaine de la section cherchée l’union de ceux des sections qui passent par  en
en  , a) permettant de vérifier qu’elle y est bien définie, ainsi que l’unicité.
, a) permettant de vérifier qu’elle y est bien définie, ainsi que l’unicité.
c) L’image d’une section maximale est un ouvert de . En effet, si cette image rencontre un ouvert
. En effet, si cette image rencontre un ouvert  dans lequel
dans lequel  est injectif, elle contient cet ouvert car celui-ci définit une section
est injectif, elle contient cet ouvert car celui-ci définit une section  et il suffit d’appliquer a) et la maximalité pour conclure.
et il suffit d’appliquer a) et la maximalité pour conclure.
d) Les images des sections maximales partitionnant , il coïncide avec l’une d’elles puisqu’il est connexe. D’où le résultat puisque
, il coïncide avec l’une d’elles puisqu’il est connexe. D’où le résultat puisque  est surjectif.
est surjectif.
Très clair. Je cherchais l’endroit où la preuve ne fonctionne plus lorsqu’on remplace la droite par le cercle
par le cercle  . Je suppose que c’est le point a) n’est-ce pas ?
. Je suppose que c’est le point a) n’est-ce pas ?
Je pense. L’intersection de deux « intervalles » n’est pas nécessairement connexe sur le cercle.
PS Il y a des typos dans ma preuve, désolé! (Par exemple, « lesquelles », la section est donnée par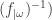 , etc.)
, etc.)
Ok, merci pour ta preuve. Au passage, j’ai réalisé le truc suivant : dans un espace connexe par arcs, si et
et  sont deux points distincts, il existe au moins un chemin allant de
sont deux points distincts, il existe au moins un chemin allant de  à
à  , mais il n’existe pas, en général, de chemin injectif allant de
, mais il n’existe pas, en général, de chemin injectif allant de  à
à  . La droite à origine dédoublée fournit un contre exemple facile (prendre pour
. La droite à origine dédoublée fournit un contre exemple facile (prendre pour  et
et  les deux origines). Probablement, la séparation de l’espace suffit pour avoir l’existence des chemins injectifs, mais c’est une autre question…
les deux origines). Probablement, la séparation de l’espace suffit pour avoir l’existence des chemins injectifs, mais c’est une autre question…
C’est une question amusante! Mais je ne sais pas y répondre en général. Sur une variété différentiable, je crois que c’est vrai. Au-delà, je ne vois pas, ce qui ne signifie pas que c’est inexact! (Loin s’en faut!)
Oui, effectivement c’est une belle question. Comme Pierre Lecomte je ne connais pas la réponse. Comme on peut se ramener à une étude locale il est clair que c’est vrai sur une variété topologique (pas forcément différentiable). Mais en général, je ne sais vraiment pas. D’ailleurs je ne connais que très peu d’exemples d’espaces non-séparés (des quotients bizarres comme la double-droite que tu mentionnes et, de manière moins académique, l’espace total du faisceau des fonctions différentiables).
MathOMan > […] il est clair que c’est vrai sur une variété topologique.
Hum, il me semble que la droite à origine dédoublée est une variété topologique (et même différentiable).
Mais non ! C’est justement pour éviter ces espaces bizarres qu’on suppose dans la définition même des variétés qu’elles sont séparées (or « Hausdorff » en allemand et anglais).
En tout il y a trois axiomes pour une variété :
1) Les cartes…
2) Espace séparé (pour ne pas avoir des choses bizarres comme la droite dédoublée)
3) Base dénombrable de la topologie (importante pour des constructions comme la partition d’unité — sinon on n’arrive pas à intégrer sur une variété différentiable…)
C’est d’ailleurs pour la même raison que dans la plupart des ouvrages « compact » ne signifie pas seulement « propriété de recouvrement », mais « propriété de recouvrement » + « séparé »…
Ok, d’accord, la droite à origine dédoublée n’est pas séparée donc ce n’est pas une variété topologique. Mais tu dis que la question est locale. Je ne vois pas pourquoi (ou alors je ne comprends pas ce que tu veux dire par là).
C’est parce qu’il faut prouver que l’ensemble des points qu’on peut relier injectivement à un point fixé préalablement est à la fois ouvert et fermé — et ce genre de preuve est toujours local… Je t’écrirai les détails ce soir 😉
Voilà, je l’ai écrit ici car c’est un peu long et je maîtrise mieux la mise en page sur mon site.
D’ailleurs il et intéressant de noter que la condition « séparé » est nécessaire, mais qu’il existe des espaces non-séparés ayant quand-même la propriété d’arcs injectifs : par exemple, le plan dédoublé à l’origine…
Merci, je vais lire les détails. Mais je suppose que tu voulais dire que la condition «séparé» n’est pas nécessaire comme le prouve le plan à origine dédoublée.
Oui, bien sûr ! D’ailleurs je viens d’apporter qqs clarifications à ma preuve…
Salut,
je trouve ce problème d’arc injectif très intéressant. Je crois que le cas d’une variété topologique est effectivement clair (je n’ai pas pris le temps de regarder la preuve de MathOman en détails mais l’idée a l’air juste). Concernant le cas général, je ne sais pas s’il est vrai ou non. S’il est vrai, j’ai peut-être une bonne idée pour sa preuve.
L’idée est la suivante. On considère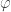 une application continue de
une application continue de ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) dans un espace topologique séparé
dans un espace topologique séparé  . Le défaut d’injectivité peut être interprété comme l’existence de lacets induits par
. Le défaut d’injectivité peut être interprété comme l’existence de lacets induits par 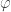 . C’est-à-dire que si
. C’est-à-dire que si  , alors
, alors 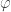 restreint à
restreint à ![[t_1,t_2]](https://s0.wp.com/latex.php?latex=%5Bt_1%2Ct_2%5D&bg=ffffff&fg=333333&s=0&c=20201002) est un lacet en
est un lacet en  . Il faudrait donc « couper » ces lacets. Pour cela, on construit par récurrence une suite de
. Il faudrait donc « couper » ces lacets. Pour cela, on construit par récurrence une suite de 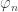 en « coupant » étapes par étapes les lacets du plus long au plus court lacets. Pour « couper » le lacet, on remplace le lacet par une constante sur l’intervalle correspondant. Par la suite, on ne s’occupe plus des lacets situés sur cet intervalle; on « coupe » les lacets situés en dehors de cet intervalle. Un tel procédé peut ne pas s’arrêter. Cependant, on peut constater (il me semble) que
en « coupant » étapes par étapes les lacets du plus long au plus court lacets. Pour « couper » le lacet, on remplace le lacet par une constante sur l’intervalle correspondant. Par la suite, on ne s’occupe plus des lacets situés sur cet intervalle; on « coupe » les lacets situés en dehors de cet intervalle. Un tel procédé peut ne pas s’arrêter. Cependant, on peut constater (il me semble) que 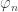 converge simplement. En effet, si
converge simplement. En effet, si  n’est pas une suite constante, elle ne varie qu’une fois (il ne faut pas oublier que l’on « coupe » les lacets en allant du plus grand au plus petit). J’appelle
n’est pas une suite constante, elle ne varie qu’une fois (il ne faut pas oublier que l’on « coupe » les lacets en allant du plus grand au plus petit). J’appelle  la limite de la suite
la limite de la suite  .
.
Il y a maintenant deux questions dont je ne suis pas sûr de la réponse : est-elle continue? Je pense que oui.
est-elle continue? Je pense que oui.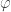 et
et  se lit sur une famille dénombrable de segments disjoints dont la longueur tend vers
se lit sur une famille dénombrable de segments disjoints dont la longueur tend vers  . Sur ces segments,
. Sur ces segments,  est constante. En quotientant
est constante. En quotientant ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) par ces segments, chacun de ces segments étant une classe d’équivalence, on devrait obtenir une application injective et continue si la réponse à la question 1 est vraie. La question est donc : le quotient de
par ces segments, chacun de ces segments étant une classe d’équivalence, on devrait obtenir une application injective et continue si la réponse à la question 1 est vraie. La question est donc : le quotient de ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) obtenu est-il homéomorphe à
obtenu est-il homéomorphe à ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) ? Des exemples comme l’escalier du diable me font douter car cela suggère l’existence de situation plutôt complexe. Cependant, l’ensemble obtenu devrait être ordonné, non dénombrable, connexe, compact,… non?
? Des exemples comme l’escalier du diable me font douter car cela suggère l’existence de situation plutôt complexe. Cependant, l’ensemble obtenu devrait être ordonné, non dénombrable, connexe, compact,… non?
1)
2) L’écart entre
Dites-moi ce que vous en pensez?
Salut Ludo, (je laisse deviner la topologie, disons simplement que
(je laisse deviner la topologie, disons simplement que 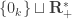 s’identifie à
s’identifie à  ) : je pense au chemin
) : je pense au chemin ![f:[0,1]\to X](https://s0.wp.com/latex.php?latex=f%3A%5B0%2C1%5D%5Cto+X&bg=ffffff&fg=333333&s=0&c=20201002) tel que
tel que  ,
,  si
si 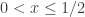 ,
,  si
si 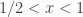 et
et  . Ce chemin là est amusant car
. Ce chemin là est amusant car 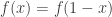 pour tout
pour tout ![x\in ]0,1[](https://s0.wp.com/latex.php?latex=x%5Cin+%5D0%2C1%5B&bg=ffffff&fg=333333&s=0&c=20201002) , alors comment coupe-t-on le plus grand lacet ? 😀
, alors comment coupe-t-on le plus grand lacet ? 😀
J’ai fait la même constatation que toi. Mais il faudra utiliser une hypothèse de séparation, car si on regarde le chemin le plus naturel reliant les deux origines de la demi-droite à origine dédoublée
C’est bien pour ça que je fais l’hypothèse de séparation. Pour que l’on puisse « couper » les lacets en commençant par un plus grand, il faut qu’il y ait un plus grand lacet. Dans ton cas, il n’y a pas de plus grand lacet. Pour cela, j’utilise le fait que la diagonale de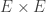 soit un fermé (Cette propriété est équivalente à la séparation T2, non?). Dans ton cas, la diagonale n’est pas non plus fermée.
soit un fermé (Cette propriété est équivalente à la séparation T2, non?). Dans ton cas, la diagonale n’est pas non plus fermée.
Je n’ai pas justifié l’existence de ce plus grand lacet. Je précise l’idée. Il suffit de considérer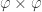 (ie. :
(ie. :  ). Cette application est continue. L’image réciproque
). Cette application est continue. L’image réciproque 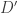 de la diagonale par cette application est un sous-ensemble compact de
de la diagonale par cette application est un sous-ensemble compact de ![[0,1]\times [0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5Ctimes+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Ensuite, la distance usuelle sur
. Ensuite, la distance usuelle sur ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) est définie et continue sur
est définie et continue sur ![[0,1]\times [0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5Ctimes+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Elle atteint donc un maximum en restriction au compact
. Elle atteint donc un maximum en restriction au compact 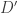 . Un couple réalisant ce maximum correspond à ce que j’appelle un plus grand lacet de
. Un couple réalisant ce maximum correspond à ce que j’appelle un plus grand lacet de 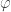 .
.
Oui, je pense que diagonale fermée équivaut à la séparation à la Hausdorff.
Au départ j’avais la même idée que Ludovic, c’est-à-dire rendre un chemin injectif en enlevant les parties où il ne l’est pas. Puis, en pensant aux horribles courbes de Jordan je commencais avoir peur ! C’est pourquoi je me suis borné au cas dont je pouvais forunir une preuve 100% sûr (variété topologique). Il faudrait essayer d’exploiter l’idée de Ludovic pour voir si elle fonctionne. Ici le diable me semble caché dans le détail. Les espaces généraux et les applications continues peuvent nous réserver bien de surprises… 😉
Salut,
J’ai réfléchi ce midi sur la continuité de la fonction limite. Je n’ai pas trouvé de démonstration simple. Pour cela, il faut démontrer le lemme suivant : une fonction continue de
une fonction continue de ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) dans
dans  .
.![(I_n)_{n \in \mathbb N} =([a_n,b_n])_{n \in \mathbb N}](https://s0.wp.com/latex.php?latex=%28I_n%29_%7Bn+%5Cin+%5Cmathbb+N%7D+%3D%28%5Ba_n%2Cb_n%5D%29_%7Bn+%5Cin+%5Cmathbb+N%7D&bg=ffffff&fg=333333&s=0&c=20201002) une suite de segments disjoints tels que
une suite de segments disjoints tels que 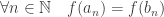 . On note :
. On note : 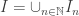 . Soit
. Soit  la fonction définie sur
la fonction définie sur ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) par :
par :
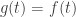 si
si  et
et  si
si  . Alors
. Alors  est continue.
est continue.
Soit
Soit
preuve :
Soit un fermé de
un fermé de  .
. est un fermé de
est un fermé de ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
. est séquentiellement fermé.
est séquentiellement fermé.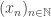 une suite à valeurs dans
une suite à valeurs dans  . qui converge vers
. qui converge vers ![x \in [0,1]](https://s0.wp.com/latex.php?latex=x+%5Cin+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.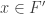 .
.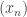 est à valeurs dans
est à valeurs dans  .
.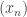 est à dans
est à dans 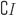 .
.
Montrons que
Il suffit de montrer que
Soit
On veut montrer que
Quitte à extraire une sous-suite, on a deux cas :
– 1er cas :
– 2eme cas :
On traite le premier cas : , on note
, on note  l’entier tel que
l’entier tel que 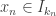 .
.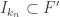 .
.
Pour tout
Remarquons que
On a deux sous-cas toujours quitte à extraire une sous-suite :
1er sous-cas : est bornée.
est bornée.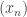 est à valeurs dans une union finie de segments inclus dans
est à valeurs dans une union finie de segments inclus dans  . Donc,
. Donc, 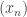 converge dans cette union et donc dans
converge dans cette union et donc dans  . Par conséquent,
. Par conséquent, 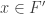
Dans ce cas,
2eme sous-cas : diverge vers
diverge vers 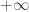 .
.
On a :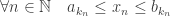 .
.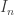 tend nécessairement vers
tend nécessairement vers  . Ainsi,
. Ainsi, 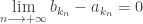 . Par conséquent, on obtient :
. Par conséquent, on obtient : 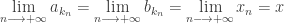 .
.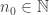 tel que
tel que 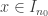 , alors, à partir d’un certain rang,
, alors, à partir d’un certain rang, 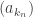 ou
ou 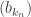 est à valeurs dans
est à valeurs dans 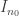 , ce qui est absurde. Donc,
, ce qui est absurde. Donc,  .
.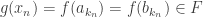 converge vers
converge vers 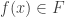 car
car  est continue. Puisque
est continue. Puisque  ,
, 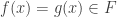 . D’où :
. D’où : 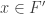 .
.
Remarquons que la longueur des segments
S’il existe
On a :
Cela termine le premier cas.
Deuxième cas :
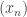 est à valeurs dans
est à valeurs dans 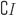 . On traite deux sous-cas :
. On traite deux sous-cas :
1er sous-cas :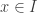 , i.e. : il existe
, i.e. : il existe 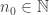 tel que
tel que 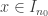 .
.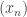 est à valeurs dans
est à valeurs dans 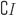 ,
, ![\forall n \in \mathbb N \quad x_n \not\in I_{n_0}=]a_{n_0},b_{n_0}[](https://s0.wp.com/latex.php?latex=%5Cforall+n+%5Cin+%5Cmathbb+N+%5Cquad+x_n+%5Cnot%5Cin+I_%7Bn_0%7D%3D%5Da_%7Bn_0%7D%2Cb_%7Bn_0%7D%5B&bg=ffffff&fg=333333&s=0&c=20201002) . On en déduit :
. On en déduit :  ou
ou 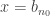 .
.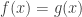 .
.
Puisque
On a donc :
2eme sous-cas : donc
donc 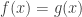 .
.
Dans tous les cas, on a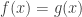 . Or,
. Or, 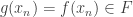 converge vers
converge vers 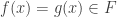 . Donc :
. Donc : 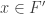 .
.
En prenant en compte tous les cas, on a obtenu :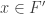 . L’ensemble
. L’ensemble  est donc fermé. La fonction
est donc fermé. La fonction  est continue.
est continue.
Une petite erreur dans le deuxième cas, 1er sous-cas, il faut lire :![x_n \not\in \stackrel{\circ}{I}_{n_0}=]a_{n_0},b_{n_0}[](https://s0.wp.com/latex.php?latex=x_n+%5Cnot%5Cin+%5Cstackrel%7B%5Ccirc%7D%7BI%7D_%7Bn_0%7D%3D%5Da_%7Bn_0%7D%2Cb_%7Bn_0%7D%5B&bg=ffffff&fg=333333&s=0&c=20201002)
Rien à dire, ce lemme tient la route ! Maintenant il ne reste qu’à exhiber la suite des intervalles I_n pour un arc donné, et le tour me semble joué et ma preuve du cas particulier des variétés deviendra superflue.
Ok. Après je suppose que tu vas «découper» les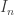 pour obtenir une fonction injective. Tu fais ça comment ? (il faut sans doute montrer au passage que
pour obtenir une fonction injective. Tu fais ça comment ? (il faut sans doute montrer au passage que ![[0,1]\setminus I](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5Csetminus+I&bg=ffffff&fg=333333&s=0&c=20201002) n’est pas vide !).
n’est pas vide !).
P.S. pour écrire , il faut écrire :
, il faut écrire :
et non :
Je ne sais pas pourquoi.
Je pense que l’idée de découper suivant les intervalles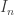 n’est pas bonne. Par exemple, pour l’escalier du diable,
n’est pas bonne. Par exemple, pour l’escalier du diable, ![[0,1] \setminus I](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D+%5Csetminus+I&bg=ffffff&fg=333333&s=0&c=20201002) est d’intérieur vide. Cela ne marcherait donc pas.
est d’intérieur vide. Cela ne marcherait donc pas.![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) par la relation :
par la relation : 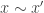 si il existe
si il existe 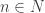 tel que
tel que 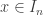 et
et 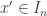 ou si
ou si 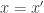 . J’espère que l’espace topologique quotient obtenu est homéomorphe à
. J’espère que l’espace topologique quotient obtenu est homéomorphe à ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) (ce n’est pas encore fait). Dans le cadre plus général du lemme, je ne suis pas sûr que ce soit vrai. Mon principal problème est que je ne connais pas de caractérisation topologique de
(ce n’est pas encore fait). Dans le cadre plus général du lemme, je ne suis pas sûr que ce soit vrai. Mon principal problème est que je ne connais pas de caractérisation topologique de ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Comme je l’ai indiqué (plus ou moins), je pense quotienté
Pour la construction de la suite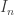 , j’ai déjà indiqué comment faire. Je peux préciser l’idée :
, j’ai déjà indiqué comment faire. Je peux préciser l’idée :![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . On peut affirmer de la même façon que : si
. On peut affirmer de la même façon que : si  est un compact de
est un compact de ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) et
et 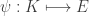 une application continue avec
une application continue avec  séparé, alors
séparé, alors  admet au moins un plus grand lacet.
admet au moins un plus grand lacet.
Tout d’abord, l’argument sur l’existence d’un plus grand lacet que j’ai déjà donné (message n°18) s’appuie essentiellement sur la compacité de
On construit une suite de segments disjoints de
de segments disjoints de ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) tel que,
tel que,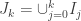 et
et ![\mathcal{J}_k=[0,1] \setminus \stackrel{\circ}{J}_k](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BJ%7D_k%3D%5B0%2C1%5D++%5Csetminus+%5Cstackrel%7B%5Ccirc%7D%7BJ%7D_k&bg=ffffff&fg=333333&s=0&c=20201002) ,
, 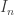 est un plus grand lacet de
est un plus grand lacet de  .
.
en notant
1) Initialisation :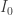 désigne le plus grand lacet de
désigne le plus grand lacet de  . On a
. On a ![I_0 \neq [0,1]](https://s0.wp.com/latex.php?latex=I_0+%5Cneq+%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) car, par hypothèse,
car, par hypothèse, 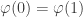 .
.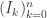 .
.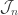 est un compact. Il admet un plus grand lacet.
est un compact. Il admet un plus grand lacet. est injectif.
est injectif. admet un plus grand lacet suivant l’intervalle
admet un plus grand lacet suivant l’intervalle  . Ce lacet est nécessairement inclus dans une composante connexe de
. Ce lacet est nécessairement inclus dans une composante connexe de  . Sinon, on aurait pu construire un lacet strictement plus grand à l’étape précédente.
. Sinon, on aurait pu construire un lacet strictement plus grand à l’étape précédente.
2) On suppose avoir construit
L’ensemble
On traite deux cas :
a)
Dans ce cas, la construction s’arrête là. On découpe suivant les intervalles et on recolle. On a obtenu notre application injective.
b) Sinon,
On peut donc construire notre suite . A défaut, la suite est finie et le résultat recherché est clair.
. A défaut, la suite est finie et le résultat recherché est clair.
Je propose de continuer cette étude. J’appelle![X=[0,1] \slash \sim](https://s0.wp.com/latex.php?latex=X%3D%5B0%2C1%5D+%5Cslash+%5Csim&bg=ffffff&fg=333333&s=0&c=20201002) où $\latex \sim$ est la relation d’équivalence que j’ai cité précédemment. Je n’ai pas écrit tous les détails mais il me semble que l’on a les faits suivants :
où $\latex \sim$ est la relation d’équivalence que j’ai cité précédemment. Je n’ai pas écrit tous les détails mais il me semble que l’on a les faits suivants :
1) Puisque les classes d’équivalences sont des segments, l’ordre sur![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) est compatible avec
est compatible avec 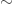 . Il induit donc un ordre total sur
. Il induit donc un ordre total sur  qui lui même caractérise la topologie de
qui lui même caractérise la topologie de  .
.
2) Le lemme que j’ai proposé nous fournit à partir de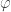 une application
une application ![g : [0,1] \longrightarrow E](https://s0.wp.com/latex.php?latex=g+%3A+%5B0%2C1%5D+%5Clongrightarrow+E&bg=ffffff&fg=333333&s=0&c=20201002) . Cette application est compatible avec la relation
. Cette application est compatible avec la relation 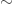 . On peut donc relever
. On peut donc relever  en une application continue
en une application continue 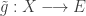 . Puisque, à chaque étapes, nous avons construit
. Puisque, à chaque étapes, nous avons construit 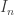 de tel sorte qu’il soit maximal et qu’il est clair que la longueur des segments
de tel sorte qu’il soit maximal et qu’il est clair que la longueur des segments 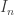 converge vers 0, l’application
converge vers 0, l’application  est injective. La continuité et l’injectivité ainsi que la séparation de
est injective. La continuité et l’injectivité ainsi que la séparation de  impose que
impose que  soit séparé. Puisque
soit séparé. Puisque  est un quotient de
est un quotient de ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) , on en déduit que
, on en déduit que  est compact.
est compact.
3) Puisque![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) est contractile,
est contractile,  doit l’être également.
doit l’être également.
Salut Ludo,![\mathcal P=([a_n,b_n])_{n\in\mathbf N}](https://s0.wp.com/latex.php?latex=%5Cmathcal+P%3D%28%5Ba_n%2Cb_n%5D%29_%7Bn%5Cin%5Cmathbf+N%7D&bg=ffffff&fg=333333&s=0&c=20201002) est une partition infinie dénombrable de
est une partition infinie dénombrable de ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) par des segments non vides (
par des segments non vides (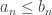 ) alors le quotient
) alors le quotient ![X=[0,1]/\sim_{\mathcal P}](https://s0.wp.com/latex.php?latex=X%3D%5B0%2C1%5D%2F%5Csim_%7B%5Cmathcal+P%7D&bg=ffffff&fg=333333&s=0&c=20201002) (où
(où  est la relation d’équivalence dont tu parles) est homéomorphe à
est la relation d’équivalence dont tu parles) est homéomorphe à ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Mais je pense que ce n’est pas tout à fait trivial. Rien que le fait que
. Mais je pense que ce n’est pas tout à fait trivial. Rien que le fait que  n’est pas fini ne me paraît pas tout à fait immédiat.
n’est pas fini ne me paraît pas tout à fait immédiat.
Je pense aussi que si
Si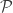 est une partition dénombrable et infinie de
est une partition dénombrable et infinie de ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) , alors
, alors  est dénombrable et infini, non?
est dénombrable et infini, non?
P.S. : Il me semble que la définition « classique » d’une partition impose que les ensembles de la partition soient non vide. Ce qui est sous-jacent est que les ensembles de la partition doivent être les classes d’équivalence d’une relation d’équivalence. En pratique, on se le permet quand même. J’ai eu cette discussion avec des collègues cette année.
Oups, j’aurais mieux fait de dire : «le fait que n’est pas dénombrable ne me paraît pas tout à fait immédiat» 🙂
n’est pas dénombrable ne me paraît pas tout à fait immédiat» 🙂 n’est pas une partition de
n’est pas une partition de ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . La partition est obtenue quand on ajoute tous les singletons
. La partition est obtenue quand on ajoute tous les singletons  où
où ![x\in [0,1]\setminus \bigcup_{n\in\mathbf N} [a_n,b_n]](https://s0.wp.com/latex.php?latex=x%5Cin+%5B0%2C1%5D%5Csetminus+%5Cbigcup_%7Bn%5Cin%5Cmathbf+N%7D+%5Ba_n%2Cb_n%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Désolé.
. Désolé.
Et surtout,
P.S. je crois qu’il n’existe pas de partition dénombrable de![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) formée de segments, mais c’est une autre histoire.
formée de segments, mais c’est une autre histoire.
Pour revenir au message 25, il y a quelques erreurs de frappe :
1) Initialisation : c’est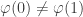
Ce n’est pas la restriction à![\mathcal{J}_k=[0,1] \setminus \stackrel{\circ}{J}_k](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BJ%7D_k%3D%5B0%2C1%5D++%5Csetminus+%5Cstackrel%7B%5Ccirc%7D%7BJ%7D_k&bg=ffffff&fg=333333&s=0&c=20201002) qui peut être injective mais celle à
qui peut être injective mais celle à ![[0,1] \setminus [a_k,b_k[](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D++%5Csetminus+%5Ba_k%2Cb_k%5B&bg=ffffff&fg=333333&s=0&c=20201002) car
car 
> Ludovic dit : Je pense que l’idée de découper suivant les intervalles n’est pas bonne.
Pourquoi ? Enlever chaque intervalle de non-injectivité puis recoller les bords, c’est précisément la même chose que faire ton quotient.
Message 29, Pierre dit : je crois qu’il n’existe pas de partition dénombrable de [0,1] formée de segments, mais c’est une autre histoire.
Tiens, je crois le contraire !
D’abord on prend [0,1/3] et [2/3,1].
Il reste donc à partitionner ]1/3,2/3[ ; on prend alors [4/9,5/9].
Il reste ]1/3,4/9[ et ]5/9,2/3[ ; on prend alors [10/27,11/27] et [16/27,17/27].
Etc.
PS: En plus, il n’existe pas de partition non-dénombrable de [0,1] formée de segments non-réduits à des points.
En effet, chaque tel segmant contiendrait un rationnel et les rationnels sont dénombrables.
Je reviens à une partition dénombrable de![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) formée de segments : je pense que tu seras d’accord de modifier un peu ta construction ainsi (pour simplifier). Au départ, on prend
formée de segments : je pense que tu seras d’accord de modifier un peu ta construction ainsi (pour simplifier). Au départ, on prend ![[1/3,2/3]](https://s0.wp.com/latex.php?latex=%5B1%2F3%2C2%2F3%5D&bg=ffffff&fg=333333&s=0&c=20201002) , ensuite
, ensuite ![[1/9,2/9]](https://s0.wp.com/latex.php?latex=%5B1%2F9%2C2%2F9%5D&bg=ffffff&fg=333333&s=0&c=20201002) et
et ![[7/9,8/9]](https://s0.wp.com/latex.php?latex=%5B7%2F9%2C8%2F9%5D&bg=ffffff&fg=333333&s=0&c=20201002) , etc.
, etc.
Dans cette construction :
les extrémités des intervalles choisis sont triadiques : l’équivalent des nombres décimaux en base trois.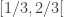 (resp.
(resp. ![[1/9,2/9]](https://s0.wp.com/latex.php?latex=%5B1%2F9%2C2%2F9%5D&bg=ffffff&fg=333333&s=0&c=20201002) ,
, ![[7/9,8/9]](https://s0.wp.com/latex.php?latex=%5B7%2F9%2C8%2F9%5D&bg=ffffff&fg=333333&s=0&c=20201002) ) sont les nombres dont l’écriture en base trois est de la forme
) sont les nombres dont l’écriture en base trois est de la forme 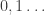 (resp.
(resp.  ,
, 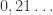 ).
).
les nombres intérieurs aux intervalles choisis ont au moins un chiffre 1 dans l’écriture triadique. Par exemple, les éléments de
Il me semble donc que le nombre qui s’écrit en base trois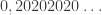 (qui vaut sauf erreur
(qui vaut sauf erreur 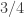 ) n’est dans aucun des intervalles choisis, donc on n’a pas une partition.
) n’est dans aucun des intervalles choisis, donc on n’a pas une partition.
Tu as raison, j’étais un peu trop vite ! Alors, comment démontre-t-on qu’il n’y a pas de partition dénombrable en forme de segments ?
En ce qui concerne la question initiale et l’idée de la preuve de Ludovic, ça ne semble pas gagné (car les points omis par « ma quasi-partition » forment un ensemble de mesure nulle)…
Effectivement, il y a des fautes de frappes. Il faut modifier les en
en 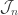 et puis,
et puis, 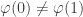 .
.
Il y a également une erreur dans la construction. Je pensais que l’ensemble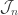 permettait de simplifier la construction mais la remarque de MathoMan est juste;
permettait de simplifier la construction mais la remarque de MathoMan est juste; 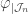 ne peut être injectif. Il faut donc rectifier la construction. C’est surtout un problème de rédaction.
ne peut être injectif. Il faut donc rectifier la construction. C’est surtout un problème de rédaction.
Concernant l’exemple de MathOMan, l’escalier du diable est justement une fonction de![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) vers
vers ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) continue, croissante bijective et constante sur chacun des intervalles que tu proposes. Dans ce cas, le quotient obtenu est homéomorphe à
continue, croissante bijective et constante sur chacun des intervalles que tu proposes. Dans ce cas, le quotient obtenu est homéomorphe à ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Cette situation est donc tout à fait possible.
. Cette situation est donc tout à fait possible.
La construction de l’homéomorphisme peut peut-être se faire par la construction d’un escalier du diable adapté aux intervalles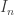 . Je vais y réfléchir.
. Je vais y réfléchir.
Je reprends la question de montrer que si un espace séparé M est connexe par arcs alors deux points distincts peuvent être joints par un chemin injectif. Les messages qui précèdent montrent qu’en éliminant un nombre dénombrable de boucles, on peut supposer que l’on a un chemin![f: [0,1]\to M](https://s0.wp.com/latex.php?latex=f%3A+%5B0%2C1%5D%5Cto+M&bg=ffffff&fg=333333&s=0&c=20201002) vérifiant
vérifiant  constante sur
constante sur ![[x,y]](https://s0.wp.com/latex.php?latex=%5Bx%2Cy%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Soit ~ la relation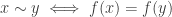 . Soit
. Soit ![X=[0,1]/\sim](https://s0.wp.com/latex.php?latex=X%3D%5B0%2C1%5D%2F%5Csim&bg=ffffff&fg=333333&s=0&c=20201002) . Alors f se factorise en une injection continue g de X dans M, donc on voit déjà que X est séparé, et de plus c’est un quotient d’un compact donc X est compact. Il suffit donc de montrer que X est homéomorphe à [0,1].
. Alors f se factorise en une injection continue g de X dans M, donc on voit déjà que X est séparé, et de plus c’est un quotient d’un compact donc X est compact. Il suffit donc de montrer que X est homéomorphe à [0,1].
Pour cela, il suffit par compacité de trouver une bijection continue de X dans [0,1].
Soit U l’ensemble des x tels que f soit constante au voisinage de x. C’est un ouvert de [0,1].
Soit Y le complémentaire de U dans [0,1]. Il est compact et parfait (=sans point isolé).
Supposons trouvé une mesure de probabilité diffuse (=dont la masse de tout point est nulle) m dont le support est Y. Posons h(x)=m([0,x]). C’est une fonction continue croissante telle que h(0)=0 et h(1)=1. De plus, pour tous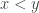 ,
,
On se ramène donc à montrer que pour tout espace métrique compact parfait Y, il existe une mesure de probabilité diffuse de support Y.
D’abord, il existe une mesure de probabilité diffuse sur Y. En effet, il est connu que Y contient une partie homéomorphe à l’ensemble de Cantor C. De plus, la mesure image de la mesure de Lebesgue sur [0,1] par l’application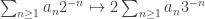 de [0,1] dans C est une mesure de probabilité diffuse sur C (où
de [0,1] dans C est une mesure de probabilité diffuse sur C (où 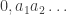 est le développement en base 2 d’un réel compris entre 0 et 1).
est le développement en base 2 d’un réel compris entre 0 et 1).
Revenons à la preuve. Pour tout n, Y est recouvert par un nombre fini N(n) de boules ouvertes de rayon 1/n. Soient Y(n,i) les adhérences de ces boules. Ce sont des espaces métriques compacts parfaits donc d’après le paragraphe précédent il existe des mesures de probabilité diffuses m(n,i) sur Y(n,i). Soit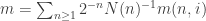 , alors m est une mesure de probabilité diffuse sur Y dont le support rencontre chacun des Y(n,i), donc son support est Y.
, alors m est une mesure de probabilité diffuse sur Y dont le support rencontre chacun des Y(n,i), donc son support est Y.
C’est joli. Et ça donne envie de se remettre à l’analyse ! 🙂
Finalement la chose la plus difficile qui est utilisée (?), c’est l’existence de la mesure de Lebesgue sur [0,1].
Je remonte un peu le sujet de loin mais pour répondre à :
> Alors, comment démontre-t-on qu’il n’y a pas de partition dénombrable en forme de segments ?
On peut trouver une forme beaucoup plus générale de ce résultat dans Bourbaki. Voir par exemple http://www.madore.org/~david/misc/best_of_GroTeXdieck/topo pour l’énoncé et une démonstration.
Oui 🙂
J’y étais revenu un peu plus tard : ici.