Dans un commentaire, Math O’Man demandait comment on démontre que n’admet pas de partition non triviale en segments
avec
. Voici une solution que j'espère correcte.
Soit une telle partition. L'ensemble
est évidemment (au plus) dénombrable. On munit
de la topologie quotient. Grâce à la surjection continue
, on peut affirmer que
est quasi-compact (i.e. «compact mais peut-être pas séparé a priori»).
En fait en fait elle ne coïncide pas, cette preuve est corrigée dans les commentaires est séparé car il est ordonnable au sens où il existe une relation d’ordre total (je vous laisse deviner laquelle !) sur
dont la topologie associée coïncide (je devrais écrire la vérification…)
avec la topologie de . J’utilise ici le fait que la topologie associée à une relation d’ordre total (celle qui est engendrée par les intervalles ouverts) est toujours séparée. Ainsi est compact, donc localement compact, et donc de Baire. De plus
est connexe, grâce à la surjection
. Or on a le lemme évident :
Lemme. Un espace de Baire séparé, dénombrable et connexe a au plus un point.
En effet, chaque singleton est fermé (car l’espace est séparé). Si l’espace a au moins deux points, chaque singleton
est d’intérieur vide (sinon
est un ouvert fermé non trivial ce qui contredit la connexité), donc l’espace est une réunion dénombrable de fermés d’intérieur vide, c’est absurde puisqu’il est de Baire.
Conclusion est un singleton, la partition est triviale, c.q.f.d. Il y a sûrement une preuve dans un jargon moins pompeux, avec seulement des suites et de la compacité par exemple… Généralisation : on peut montrer que le plan
n’est pas une réunion de disques fermés disjoints de rayons strictement positifs. Mais il y a un énoncé beaucoup plus général :
Théorème. Aucun espace localement compact, connexe et localement connexe, n’est la réunion disjointe d’une suite finie ou infinie d’au moins deux fermés non vides.
C’est un exercice que l’on trouve dans le traité de topologie de Bourbaki au sujet des espaces topologiques dits totalement inépuisables ! Donc, si l’on vous demande de paver un carré (plein) de façon non triviale avec des rectangles, des triangles, des cercles disques, etc., tous pleins et fermés, vous savez que ce n’est pas possible car le carré est localement compact, connexe et localement connexe.
Tout cela peut faire penser à un certain sujet d’agrégation de mathématiques (je ne sais plus l’année) où l’on montrait que le plan n’est pas une réunion disjointes de cercles, mais que l’espace
en est une ! Bien sûr, rien de ce qui précède ne s’applique pour ces problèmes de cercles car les partitions considérées ne sont pas dénombrables.

Très clair, merci !
Quand tu écris « des triangles, des cercles, etc., tous pleins et fermés », veux-tu dire par « cercles pleins » que ce sont des disques ?
Oui, je vais corriger cette erreur !
« Montrer qu’un espace affine euclidien de dimension 3 est réunion disjointe de cercles », c’était l’objet de la partie II de ce sujet de l’agrégation de mathématiques en 1998 : http://agreg.org/sujets/M98AD1E.PDF
🙂
Je vais faire les vérifications qui manquent à l’article. Dans la suite, si est un ensemble totalement ordonné, il est toujours muni de la topologie engendrée par les intervalles ouverts (en fait les ouverts sont les unions d’intervalles ouverts). On dit qu’une partie de
est un ensemble totalement ordonné, il est toujours muni de la topologie engendrée par les intervalles ouverts (en fait les ouverts sont les unions d’intervalles ouverts). On dit qu’une partie de  est convexe si, lorsqu’elle contient deux points, elle contient aussi l’intervalle qui a ces deux points pour extrémités.
est convexe si, lorsqu’elle contient deux points, elle contient aussi l’intervalle qui a ces deux points pour extrémités.
Proposition 1. Un ensemble totalement ordonné est séparé.
est séparé.
Preuve. Soient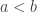 deux points distincts de
deux points distincts de  . S'il existe
. S'il existe ![c\in ]a,b[](https://s0.wp.com/latex.php?latex=c%5Cin+%5Da%2Cb%5B&bg=ffffff&fg=333333&s=0&c=20201002) alors les ouverts
alors les ouverts ![]\leftarrow,c[](https://s0.wp.com/latex.php?latex=%5D%5Cleftarrow%2Cc%5B&bg=ffffff&fg=333333&s=0&c=20201002) et
et ![]c,\rightarrow[](https://s0.wp.com/latex.php?latex=%5Dc%2C%5Crightarrow%5B&bg=ffffff&fg=333333&s=0&c=20201002) séparent
séparent  et
et  . Sinon, les ouverts
. Sinon, les ouverts ![]\leftarrow,b[](https://s0.wp.com/latex.php?latex=%5D%5Cleftarrow%2Cb%5B&bg=ffffff&fg=333333&s=0&c=20201002) et
et ![]a,\rightarrow[](https://s0.wp.com/latex.php?latex=%5Da%2C%5Crightarrow%5B&bg=ffffff&fg=333333&s=0&c=20201002) séparent
séparent  et
et  ♦
♦
Soit un ensemble totalement ordonné et soit
un ensemble totalement ordonné et soit 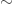 une relation d'équivalence sur
une relation d'équivalence sur  telle que les classes d'équivalence soient convexes. Les ensembles
telle que les classes d'équivalence soient convexes. Les ensembles  et
et  étant deux classes d'équivalence, on pose
étant deux classes d'équivalence, on pose  s'il existe
s'il existe  et
et  tels que
tels que  .
.
Proposition 2. La relation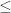 définie sur le quotient
définie sur le quotient  est une relation d’ordre total.
est une relation d’ordre total.
Preuve. Sûrement triviale… pas envie de vérifier celle-là ♦
Proposition 3. Sur le quotient , la topologie quotient coïncide avec la topologie associée à la relation d’ordre total.
, la topologie quotient coïncide avec la topologie associée à la relation d’ordre total.Preuve. à venir… mais je me demande si en écrivant la preuve, je ne vais pas trouver un contre-exemple qui montrera que j’ai raconté n’importe quoi 😐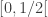 et
et ![[1/2,1]](https://s0.wp.com/latex.php?latex=%5B1%2F2%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) forment une partition de
forment une partition de ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) . L’ensemble quotient associé, muni de la topologie quotient, est grossier, donc pas séparé, et donc la topologie quotient n’est pas celle associée à la relation d’ordre évidente (puisque celle-ci est séparée). Donc, ma démonstration du fait que l’espace quotient est séparé dans l’article, est fausse. Mais je peux donner une démonstration correcte.
. L’ensemble quotient associé, muni de la topologie quotient, est grossier, donc pas séparé, et donc la topologie quotient n’est pas celle associée à la relation d’ordre évidente (puisque celle-ci est séparée). Donc, ma démonstration du fait que l’espace quotient est séparé dans l’article, est fausse. Mais je peux donner une démonstration correcte.
En effet, cette proposition 3 est fausse et il y a un contre-exemple immédiat :
Proposition 4. Soit une relation d’équivalence sur
une relation d’équivalence sur ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) telle que les classes d’équivalence soient des segments non réduits à un point et telle qu’il existe au moins deux classes d’équivalences. Alors l’espace quotient
telle que les classes d’équivalence soient des segments non réduits à un point et telle qu’il existe au moins deux classes d’équivalences. Alors l’espace quotient ![[0,1]/\sim](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%2F%5Csim&bg=ffffff&fg=333333&s=0&c=20201002) est séparé.
est séparé.
Preuve. Soient et
et  deux points du quotient. On écrit
deux points du quotient. On écrit ![A=[a,b]](https://s0.wp.com/latex.php?latex=A%3D%5Ba%2Cb%5D&bg=ffffff&fg=333333&s=0&c=20201002) et
et ![B=[c,d]](https://s0.wp.com/latex.php?latex=B%3D%5Bc%2Cd%5D&bg=ffffff&fg=333333&s=0&c=20201002) avec
avec  . Il existe un nombre entre
. Il existe un nombre entre  et
et  , et ce nombre appartient à une certaine classe d'équivalence
, et ce nombre appartient à une certaine classe d'équivalence ![[\alpha,\beta]](https://s0.wp.com/latex.php?latex=%5B%5Calpha%2C%5Cbeta%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Posons
. Posons  et
et ![V=]\beta,1]](https://s0.wp.com/latex.php?latex=V%3D%5D%5Cbeta%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) , ce sont des ouverts de
, ce sont des ouverts de ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) qui sont des unions de classes d'équivalences donc les images de
qui sont des unions de classes d'équivalences donc les images de  et
et  par la surjection canonique sont des ouverts de l'espace quotient (en effet
par la surjection canonique sont des ouverts de l'espace quotient (en effet  donc
donc  est ouvert…) et ces deux ouverts séparent
est ouvert…) et ces deux ouverts séparent  et
et  .
.
Soit Z l’ensemble des extrémités de ces intervalles privé de {0,1}. Alors Z est un espace métrique compact parfait (càd que tout point de Z est un point d’accumulation) donc Z est non dénombrable. Contradiction.
C’est bien ça 🙂 Du coup j’ai envie de faire des révisions et de chercher comment on prouve que parfait non vide implique non dénombrable !