J’ai fini par résoudre ce problème en utilisant un ordinateur et un programme écrit en Pascal (pourquoi Pascal ? parce que je commence à connaître à force d’en enseigner les bases à mes élèves). Il faut, je pense, préciser l’énoncé en disant que Pierre et Sylvain savent autant que nous que les deux ages inconnus sont compris entre 2 et 100. Introduisons quelques notations : sera l’ensemble des couples d’entiers
tels que
:
C’est un ensemble à éléments et la solution est l’un d’entre eux.
- Au début, Pierre, qui connaît le produit
, dit ne pas pouvoir déterminer
et
. Cela signifie qu’il existe un couple
, tel que
et tel que
. Notons
l’ensemble des
tels qu’il existe
, différent de
et vérifiant
. Autrement dit,
est l’ensemble des
qui sont compatibles avec la première affirmation de Pierre :
Attention : il ne suffit pas que
et
soient des nombres composés pour que
appartienne à
. Par exemple
. @Pierre Lecomte : tu n’étais donc pas tout à fait dans le vrai 😉
- Ensuite, Sylvain, qui connaît
, dit qu’il savait que Pierre ne pouvait pas déterminer
et
. Cela signifie que pour tout
vérifiant
, on a
. On notera
l’ensemble des couples
compatibles avec cette déclaration de Sylvain (et avec la première affirmation de Pierre) :
- Pierre affirme ensuite connaître la solution. Comme précédemment, on introduit l’ensemble
des couples
compatibles avec cette information et les deux précédentes. Je ne détaille pas le raisonnement qui conduit à :
- Sylvain conclut en disant qu’il connaît aussi la solution. Notons
l’ensemble des
compatibles avec les quatre informations, c’est-à-dire l’ensemble des solutions du problème :
À présent, ce n’est pas difficile d’écrire un programme qui calcule les ensembles et qui trouve donc les solutions du problème (ce sont les éléments de
). Celui que j’ai écrit contient des fonctions nommées e (resp. e1,e2,e3,e4) qui prennent en entrée un couple
et qui renvoient un booléen pour dire si le couple
est un élément de l’ensemble
(resp.
) ou pas. Je n’ai pas cherché à optimiser le programme, préférant un code plus court et plus lisible à un programme malin; par conséquent, mon code est parfois (très très) idiot, en particulier avec ses «boucles for» à 10000 itérations, toujours exécutées jusqu’au bout même lorsque la première itération fournit la réponse ! Il était demandé de trouver la solution, pas de trouver la solution rapidement 🙂
Voici ce que donne mon programme au bout de plusieurs secondes (voire plusieurs minutes) :
Comme prévu, est de cardinal un : il y a une unique solution. Je ne vais pas vous la donner, ce ne serait pas drôle. Voici juste le programme :
program enigme;
const min=2;
const max=100;
var x,y,c,c1,c2,c3,c4:integer;
function e(x,y:integer):boolean;
begin
e:=(min<=x) and (x<=y) and (y<=max);
end;
function e1(x,y:integer):boolean;
var i,j:integer;
var b:boolean;
begin
if not(e(x,y)) then e1:=false else
begin
b:=false;
for i:=min to max do
for j:=i to max do
if (i*j=x*y) and (ix) then b:=true;
e1:=b;
end;
end;
function e2(x,y:integer):boolean;
var i,j:integer;
var b:boolean;
begin
if not(e1(x,y)) then e2:=false else
begin
b:=true;
for i:=min to max do
for j:=i to max do
if (i+j=x+y) and not(e1(i,j)) then b:=false;
e2:=b;
end;
end;
function e3(x,y:integer):boolean;
var i,j:integer;
var b:boolean;
begin
if not(e2(x,y)) then e3:=false else
begin
b:=true;
for i:=min to max do
for j:=i to max do
if (i*j=x*y) and e2(i,j) and (ix) then b:=false;
e3:=b;
end;
end;
function e4(x,y:integer):boolean;
var i,j:integer;
var b:boolean;
begin
if not(e3(x,y)) then e4:= false else
begin
b:=true;
for i:=min to max do
for j:=i to max do
if (x+y=i+j) and e3(i,j) and (ix) then b:=false;
e4:=b;
end;
end;
begin
for x:=min to max do
for y:=x to max do
begin
c:=c+1;
if e1(x,y) then
begin
c1:=c1+1;
if e2(x,y) then
begin
c2:=c2+1;
if e3(x,y) then
begin
c3:=c3+1;
if e4(x,y) then
begin
c4:=c4+1;
writeln('Une solution : (',x,',',y,')');
end;
end;
end;
end;
end;
writeln('#E=',c,' #E1=',c1,' #E2=',c2,' #E3=',c3,' #E4=',c4);
end.
Pour exécuter ce programme, sous Linux, on crée un fichier, disons enigme.pas, qui contient le code, puis on compile enigme.pas grâce à la commande gpc (GNU Pascal Compiler) :
gpc -o enigme enigme.pas
On obtient un exécutable enigme que l’on peut lancer avec la commande :
./enigme
Et si vous n’avez pas installé gpc, vous pouvez le faire par la commande (sous Debian) :
apt-get install gpc
Comme pour toute installation, c’est l’utilisateur «root» qui doit lancer cette commande. Sous Ubuntu, on peut le faire depuis un compte utilisateur/administateur avec :
sudo apt-get install gpc

Ici , dans mon blog, on trouve un lien à votre deux articles et des autres liens à BibM@th et à «Une petite énigme… » par Stéphane Fischler.
Bien vu, j’aurais dû écrire et pas seulement penser. Cela aurait éviter ma faute…
PS Essayons de ne plus trop mettre »p » dans mon nom… (sans rancune)
J’ai été obligé d’écrire pour comprendre l’énoncé. De tête, je m’embrouillais rapidement !
PS : erreur corrigée, désolé.
Merci! Mais ce n’est pas bien grave.
Dans les pays de l’est, cela m’arrive souvent! En plus, ils déclinent les noms propres et c’est surprenant.
La réponse ( j’ai trouvé ce lien dans la page de Stéphane Fischler «Une petite énigme…» ) à le casse-tête «Mathématiciens et produits de nombres» — que je pense être equivalent — est 13 et 4. Si est vrai, je peux limiter à 15 les valeurs des âges.
Soit S={(x,y)∈ℕ²:2≤x≤y≤15} et S₁={(x,y)∈S:∃(i,j)∈S,ij=xy∧(i,j)≠(x,y)}.
Les produits
12=2×6=3×4
16=2×8=4×4
18=2×9=3×6
20=2×10=4×5
24=2×12=3×8=4×7
30=2×15=3×10=5×6 , …
donnent les couples
(2,6),(3,4),(2,8),(4,4), … que sont des élements de S₁.
Mais le couple (4,13)∉S₁.
Conclusion: si le probléme est équivalent et la vrai solution est 4 et 13, je ne comprens pas le principe de votre solution.
@Américo :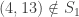 parce que tu as limité à 15 les valeurs des âges. Si on ne limite pas à 15 les valeurs des âges, on peut écrire
parce que tu as limité à 15 les valeurs des âges. Si on ne limite pas à 15 les valeurs des âges, on peut écrire 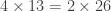 . Au début, Pierre et Sylvain ne peuvent pas réduire à 15 les valeurs des âges, car ils ne connaissent pas la réponse.
. Au début, Pierre et Sylvain ne peuvent pas réduire à 15 les valeurs des âges, car ils ne connaissent pas la réponse.
@ Pierre Bernard: Vous êtes correct, je ne peux pas limiter à 15 les valeurs des âges: (4,13)∈E₁à cause de ce que vous avez dit (4×13=2×26=52). Car j’ai lû dans la page de Stéphane Fischler « La partie difficile est de démontrer que cette solution est la seule possible», j’avais hésité avant de l’écrire. Après, j’ai aussi vu ma faute. Je suis ici ce Dimache à cette heure pour le corrigir, mais vous avez le fait avant de moi.
Le résultat n’ est pas incompatible avec la 1ère étape du votre raisonnemment, au contraire.
Dimanche
Il reste une question : peut-on résoudre le problème sans machine et en un temps raisonnable ? 🙂
J’ai essayé mais sans succès de trouver des conditions suplémentaires sans modifier le problème. Par exemple:
Si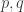 sont les deux nombres,
sont les deux nombres,  , et
, et  , on a
, on a
Mais qu’est-ce qu’on déduit de ces rélations?