Dérangements et e

Publié le par

Prenez un nombre quelconque, plutôt grand, d’objets distincts et bien rangés, chacun à sa place. Vous pouvez pensez à des livres rangés par ordre alphabétique, à un jeu de cartes bien trié, ou bien à des élèves assis dans une classe, ce n’est pas très important. Mettez un peu de désordre dans ces objets : permutez-les au hasard. Après cette expérience aléatoire, certains objets auront peut-être gardé leur position initiale. Quelle est la probabilité pour qu’aucun objet n’ait gardé sa position initiale ? Réponse : environ \dfrac{1}{e} où e=2,718\ldots est la base des logarithme népériens, le plus célèbre des nombres après {\pi}.

C’est donc un exemple(1) concret d’expérience où le nombre {e} apparaît de façon plus ou moins inattendue. On trouve aussi ce genre de chose pour le nombre \pi (voir Pile ou face et π).

Passons à l’énoncé sérieux et à sa preuve :

Définition. On appelle dérangement d’un ensemble E, toute permutation \sigma\in \mathfrak S_E sans point fixe, c.a.d. telle que \forall x\in E,\; \sigma(x)\neq x.

Dans la suite, on note, pour tout entier naturel n, {d}_n le nombre de dérangements de l’ensemble \{1,2,\ldots,n\} (qui est vide si n=0). On a (d_0,d_1,d_2,d_3,d_4,d_5,\ldots)=(1,0,1,2,9,44,\ldots). La On-Line Encyclopedia of Integer Sequences donne plus de valeurs. L’égalité {d}_{0}=1 vient du fait que l’unique permutation de l’ensemble vide est évidemment un dérangement 😀

Proposition. La suite \left( \dfrac{d_n}{n!}\right) converge vers \dfrac{1}{e}.

Démonstration. Pour tout {k}\in \{0,2,\ldots,n\}, notons E_k\subset \mathfrak S_n l’ensemble des permutations qui ont exactement k points fixes. Les ensembles E_k forment une partition de \mathfrak S_n et {E}_k possède \dbinom{n}{k} {d}_{n-k} éléments parce que définir un élément de {E}_k revient à choisir les k points fixes et à choisir une permutation sans point fixe du reste. On a donc :

\begin{displaystyle} \forall n\in\mathbf N,\quad {n}!=\sum_{k=0}^{n} \dbinom{n}{k} {d}_{n-k}\end{displaystyle}

Il s’agit d’en déduire {d}_n par une «inversion» (je dis ça parce que c’est assez analogue à la formule d’inversion de Moebius par exemple). Cette inversion se fera sous la forme d’une division de séries formelles…

\begin{displaystyle} \forall n\in\mathbf N,\quad 1=\sum_{k=0}^{n} \dfrac{1}{k!} \dfrac{{d}_{n-k}}{(n-k)!}\end{displaystyle}

On reconnaît le produit de deux séries formelles (appelé parfois produit de Cauchy) :

\begin{displaystyle} \sum_{n=0}^{+\infty} X^n=\left(\sum_{n=0}^{+\infty} \dfrac{1}{n!}X^n\right)\left(\sum_{n=0}^{+\infty} \dfrac{{d}_{n}}{n!}X^n\right)\end{displaystyle}

Remarque : on peut utiliser des séries entières à la place des séries formelles, mais c’est vraiment stupide de s’infliger des problèmes de convergence inutiles.

\begin{displaystyle} \dfrac{1}{1-X}=e^X\sum_{n=0}^{+\infty} \dfrac{{d}_{n}}{n!}X^n\end{displaystyle}

\begin{displaystyle} \dfrac{e^{-X}}{1-X}=\sum_{n=0}^{+\infty} \dfrac{{d}_{n}}{n!}X^n\end{displaystyle}

\begin{displaystyle} \left(\sum_{n=0}^{+\infty} \dfrac{(-1)^n}{n!}X^n\right)\left(\sum_{n=0}^{+\infty} X^n\right)=\sum_{n=0}^{+\infty} \dfrac{{d}_{n}}{n!}X^n \end{displaystyle}

On développe et on indentifie :

\begin{displaystyle} \forall n\in\mathbf N,\quad \sum_{k=0}^{n} \dfrac{(-1)^k}{k!}=\dfrac{{d}_n}{{n}!}\end{displaystyle}

Faisons tendre n vers +\infty :

\begin{displaystyle} e^{-1}=\lim_{n\to +\infty} \dfrac{d_n}{n!}\end{displaystyle}

D’où le résultat 🙂

Pour finir, j’ai un petit problème. On déduit facilement des calculs ci-dessus la formule suivante :

\begin{displaystyle} \forall n\in\mathbf N, \quad {d}_{n+1}=(n+1){d}_n+(-1)^{n+1}\end{displaystyle}

Je n’arrive pas à interpréter cette formule combinatoirement 😦

(1) Voici un autre exemple où {e} apparaît naturellement : on place un euro en banque à un taux de 100% et avec des «intérêts composés continus», c.a.d. que les intérêts sont incorporés au capital continuellement, les mises à jour étant faites en permanence (et pas seulement à la fin de chaque mois par exemple). Au bout d’un an, on possède e=2,718\ldots euros !

6 réflexions au sujet de « Dérangements et e »

  1. Salut Pierre,

    c’est vrai que ta formule de récurrence paraît bien étrange. En la composant deux fois, j’ai une interprétation. Cela peut peut-être donner une indication.

    On a : \begin{displaystyle} \begin{array}{ll} d_{n+2} &= (n+2) d_{n+1} + (-1)^{n+2}\\ &= (n+2) ( (n+1) d_n+ (-1)^{n+1} )+(-1)^{n+2}\\ &= (n+2) (n+1) d_n + (n+2) (-1)^{n+1}+(-1)^{n+2}\\ &= (n+2) (n+1) d_n + (n+1)(-1)^{n+1}\\ &= (n+1) ( (n+2)d_n + (-1)^{n+1} )\\ &= (n+1) ( d_{n+1} + d_n ) \end{array} \end{displaystyle}

    Cette dernière formule admet une interprétation. On veut construire un dérangement d’un ensemble à n+2 éléments. On note x le (n+2)-ième élément de l’ensemble. Il y a alors deux solutions :
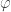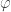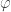    1) soit on part d’un dérangement \varphi d’un ensemble à n+1 éléments et on fixe un élément de l’ensemble y, on intercale x entre y et \varphi(y) dans le cycle de y pour la bijection \varphi. C’est-à-dire que l’on construit la bijection \tilde\varphi telle que : \tilde\varphi(y)=x, \tilde\varphi (x)=\varphi(y) sinon \tilde\varphi et \varphi sont égales.
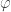    2) soit on part d’une bijection \varphi de l’ensemble à n+1 élément ayant exactement un point fixe. On construit alors le dérangement qui intervertit x et le point fixe et qui, par ailleurs, est égale à \varphi.

    Dans le premier cas, on a (n+1)d_{n+1} choix. Dans le deuxième, on a : (n+1)d_n. On retrouve bien la formule.

    Répondre ↓

  5. Juste une petite remarque concernant la « formule d’inversion » dont tu (vous) parle(z) :

    Trouver les d_n en partant de la formule n!=… revient à résoudre un bête système d’équations linéaires
    (on peut le voir comme infini ou limiter la taille à un entier N donné si on n’aime pas les matrices de taille infinies… : cela ne change rien).

    La matrice du système est en fait composée des coefficients binomiaux (complétés par des 0) et le problème revient à inverser cette matrice.
    On peut trouver cette inverse

    1) en ‘tatonant’ puis en vérifiant que le produit des deux matrices fait l’identité.

    2) en utilisant des séries comme tu le fait (vous le faîtes).

    3) (et c’est là ma remarque) en constatant que la matrice des coefficients binomiaux est l’exponentielle de la matrice N entiérement nulle sauf les termes en dessous de la diagonale qui sont 1,2,3,4,… ce qui permet de dire que son inverse est l’exponentielle de -N qui ce calcule de façon immédiate.

    Répondre ↓

Laisser un commentaire